4×4 魔術方塊基礎復原解法教學 – 簡易降階法
只要會 3×3 就能輕鬆學會的 4×4 魔術方塊教學!
工欲善其事,必先利其器,到這裡買顆好轉有磁力的 4×4 魔方更能提升復原樂趣~
教學目錄
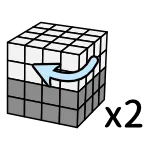
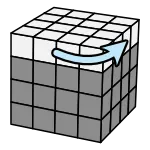
Step1 - 組中心
這階段完成時
方塊會長這樣
階段目標:把中心的 4 顆變完整,且按照標準配色處理。
把要組的中心顏色朝上方
動作都是「往上 - 往前 - 往下」
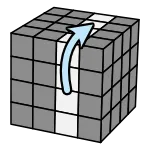
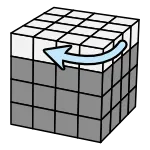
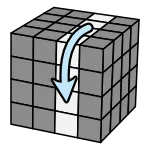
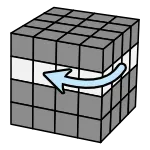
流程是把要復原的顏色轉到上方
找到目標後,放前面的右下角
轉動作就會上去了
一開始都是先組白色中心
如果有白色卡在最下面?
也是擺下面的右下角,只是往上下的動作變成轉半圈
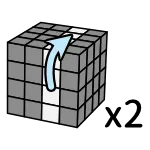

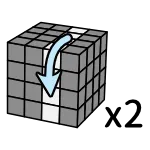
白色中心完成後組黃色
黃色在白色的對面;等黃色中心也完成後接著組其他顏色,其餘復原順序不重要,但要按照下方配色去復原。
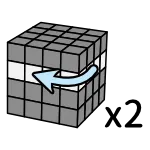
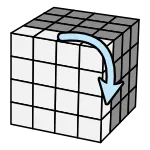
Step2 - 組邊塊
這階段完成時
方塊會長這樣
階段目標:把邊塊變整齊,同時不破壞中心。
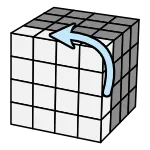
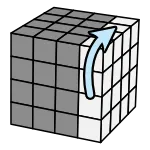
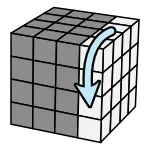
Step3 - 完整復原
這階段完成時
方塊會長這樣
階段目標:把 4x4 當成 3x3 玩。
組合中心和邊塊之後,接下來只轉最外層的話,4x4 其實就只是長得比較怪的 3x3 而已,復原方法完全相同。所以接下來按照 3x3 魔術方塊的復原流程處理即可。
只轉最外層
但是有 2 個特殊狀況
特殊狀況 - 單邊反轉
在「黃色十字」階段,黃色邊塊朝上的數量只會是 0 顆、2 顆、4 顆,不會是奇數。所以如果遇到 1 顆或 3 顆黃色邊塊朝上的情況,怎麼拿都可以 (黃色中心朝上就好),直接轉下方公式就行~
推薦學正常版轉法,如果懶得背就學簡單版吧
這是正常玩家的做法,兼顧步數與速度
建議按照箭頭分段記憶比較容易
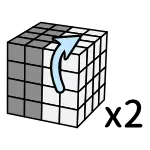
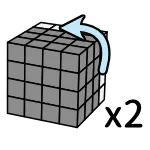
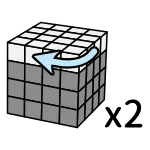
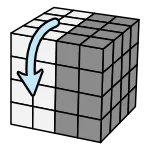

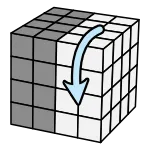

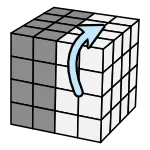

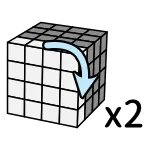


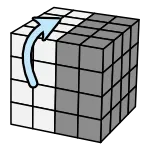


記法
右半圈、後半圈
(每次都把上面層轉半圈) 左下、右下、右上
(每次都把前面層轉半圈) 右上、左上
第一個箭頭的動作倒著做
非常容易記憶的做法,但缺點是非常慢,永遠落後人的速度


這組動作做 5 次
但是有副作用
這公式雖然解決單邊反轉這個特殊狀況,但是會順手破壞幾組邊塊,所以要退回 Step2 – 組邊塊的階段,把被破壞掉的重新組回來,再重新當 3×3 復原一次。
特殊狀況 - 對邊互換
在最後一個復原階段,如果只剩 2 顆交換就是這個狀況 (對邊交換、鄰邊交換、2 角交換都是),怎麼拿都可以 (黃色面朝上就好),直接轉下方公式就行~