在學會魔方盲解之後,掌握一套編碼系統是必要的,因為比起單純透過邊角顏色記憶,編碼可以顯著提高記憶效率!全數字編碼但運用範圍廣,可以套用到 4×4 和 5×5 盲解,善於記憶數字的玩家能發揮其價值。
編碼定義
全數字編碼是透過嚴謹的規則去編碼,基本上只要掌握下方 2 點就可以輕鬆進行:
- 對於「位置」的部分,使用數字 1、2、3、4、5、6、7、8、9、0(零)、00(百)、000(千)。
- 對於「方向」的部分,使用詞綴,朝上下的稱為 1、朝前後的稱為 2、朝左右的稱為 3。
在定義這兩個位置與方向的條件後,我們就有能力對每個點位賦予代號了。
角塊
角塊只有 8 顆,相當適合使用全數字編碼比較簡單。先套用上定義 1:
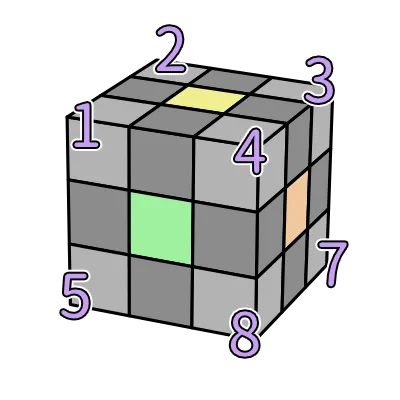
編碼的部分我習慣從上面往下看順時針的方式編列,因為現在盲解主流是盡量不做整顆轉動的 xyz,判斷上比較容易。接下來再套用定義 2:
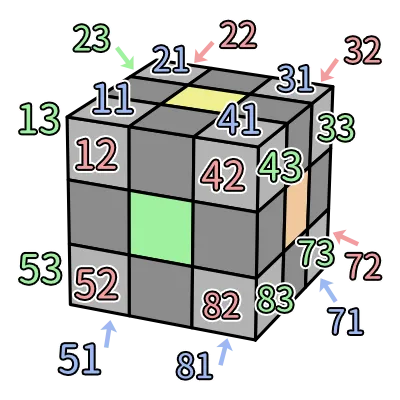
直接將定義 2 加在定義 1 的後面,這樣就完成。所以每個編碼就是二位數,不會搞混,運氣很差時也就記憶大約 16~20 位數而已,依然算是簡單。
看完角塊編碼案例後應該對於這系統的運作方式稍微有概念了,我們第一步先讀出它的位置,就好比上左前這顆我們先給個代號 1。接著更進一步讀出它的方向,這麼做就可以替上左前這顆的三個方向都製作專屬的代碼:「上左前」 的話是 11,「前上左」的話是 12,「左前上」的話是 13。
邊塊
個人認為全數字編碼不太適合用在邊塊,畢竟要記憶的資訊有點多,這部分可以參考資訊量少一倍的英數混合系統。如果一樣想要在邊塊使用全數字編碼的話,一樣也是按照順時針、從上到下先套用定義 1,接著再套用定義 2 就完成。
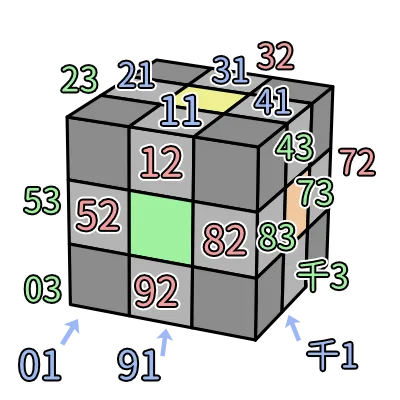
實際示範
那最後就來看個案例吧,一樣也是黃上綠前轉亂,然後也是用雙公式盲解教學的案例示範:
示範 1
- SC:R D R' U' R D' R' U
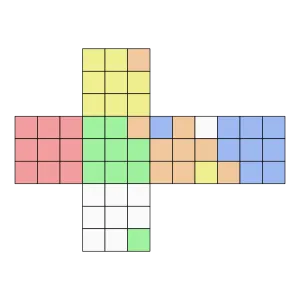
起點 (上前右,編碼 41) 通常不建議記,那個地方永遠不變的,沒有必要耗費心力記憶。所以接下來的目標結合編碼看依序是:上右後 (編碼 31)、右下後 (編碼 73)。結論是這個狀況只要記「3173」就可以結束。
示範 2
- SC:R2 U' F2 R' U R2 U2 L U F2 D2 R' D2 U' L' U2
這組比較長一些,但一樣是按照流程慢慢編碼:起點 → 左上後 (編碼 23) → 前下右 (編碼 82) → 後上右 (編碼 32) → 上左前 (編碼 11) → 左後下 (編碼 63) → 右下後 (編碼 82)。
整組循環就是 238232116382,看起來比較長對吧? 這時可以使用盲解心法 – 記憶篇提到的分段技巧,就會變成下方比較好記的方式:
2382、3211、6382。